정렬 알고리즘 기초3 - 힙 정렬(Heap Sort)
By on August 16, 2019
1. 힙정렬 알고리즘(Quick Sort)
- 우선 힙정렬을 이해하기 위해서는 이진트리 구조를 이해해야 한다.
- 이진트리
- 이진트리란 루트(root) 노드 부터 시작해서 최대 두개의 자식 노드를 가지는 트리 구조를 말한다.
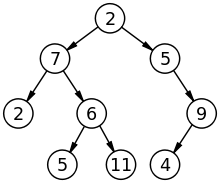
- 이진트리
-
힙(Heap) 이란 최소값이나 최대값을 빠르게 찾아내기위한 완전 이진트리를 기반으로 하는 트리입니다.
힙에는 최대 합과 최소합이 존재하는대 최대 합은 부모노드가 자식노드보다 큰합이라고 할 수 있습니다.
힙구조에서는 루트(root) 노드의 값보다 자식의 값이 클수 없습니다.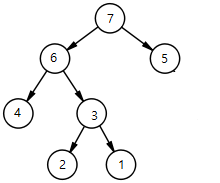
-
힙생성 알고리즘(Heapify Algorithm) 트리안에서 특정 노드때문에 최대 힙이 붕괴되는 경우가 있습니다. 아래 그림을 보면 정상적으로 힙이 구성 되어있지만
자식 노드가 부모노드보다 큰 8의 값이 들어와서 최대힙이 붕괴되어있는 모습을 볼 수 있습니다.
이때 힙생성 알고리즘(Heapify Algorithm)을 사용 하여 부모 노드보다 큰 자식의 값의 자리를 변경 합니다.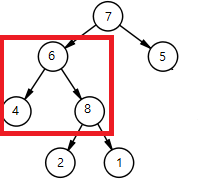
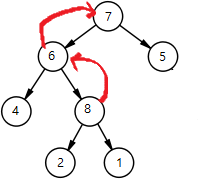
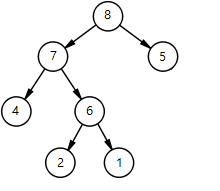
힙생성 알고리즘을 통하여 최대 힙을 항상 유지 해야 합니다.
-
정렬 순서
예1) 3,5,1,2,4,8,6,9,7 배열을 오름차순으로 정렬 하려고 할 경우1) 첫 번째로 이진트리에 삽입이 되는 순서대로 배열에 담는다.
0 1 2 3 4 5 6 7 8 3 5 1 2 4 8 6 9 7 위 배열의 이진트리는 아래 와 같다.
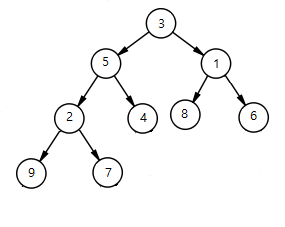
2) 힙생성 알고리즘을 수행한다.
- 배열의 {3, 5, 1} 을 정렬 한다 ==> 3과 5의 자리를 변경 한다 ==> {5, 3, 1}
- 배열의 {3, 2, 4} 을 정렬 한다 ==> 4와 3의 자리를 변경 한다 ==> {4, 2, 3}
- 배열의 {2, 9, 7} 을 정렬 한다 ==> 2와 9의 자리를 변경 한다 ==> {9, 2, 7}
- 배열의 {1, 8, 6} 을 정렬 한다 ==> 1과 8의 자리를 변경 한다 ==> {8, 1, 6}0 1 2 3 4 5 6 7 8 5 4 8 9 3 1 6 2 7 3) 힙생성 알고리즘을 수행한다.
- 배열의 {5, 4, 8} 을 정렬 한다 ==> 5와 8의 자리를 변경 한다 ==> {8, 4, 5}
- 배열의 {4, 9, 3} 을 정렬 한다 ==> 4와 9의 자리를 변경 한다 ==> {9, 4, 3}
- 배열의 {4, 2, 7} 을 정렬 한다 ==> 4와 7의 자리를 변경 한다 ==> {7, 2, 4}
- 배열의 {5, 1, 6} 을 정렬 한다 ==> 5와 6의 자리를 변경 한다 ==> {6, 1, 5}0 1 2 3 4 5 6 7 8 8 9 6 7 3 1 5 2 4 4) 힙생성 알고리즘을 수행한다.
- 배열의 {8, 9, 6} 을 정렬 한다 ==> 8과 9의 자리를 변경 한다 ==> {9, 8, 6}
- 배열의 {8, 7, 3} 을 정렬 한다 ==> 변경 없음 ==> {8, 7, 3}
- 배열의 {7, 2, 4} 을 정렬 한다 ==> 변경 없음 ==> {7, 2, 4}
- 배열의 {6, 1, 5} 을 정렬 한다 ==> 변경 없음 ==> {6, 1, 5}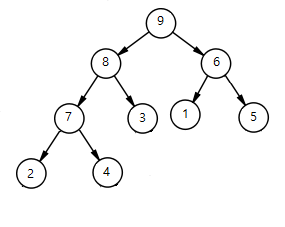
5) 정렬수행
a. 배열의 제일 처음 숫자(root node)는 항상 큰수이다.0 1 2 3 4 5 6 7 8 9 8 6 7 3 1 5 2 4
b. 처음 숫자와 가장 마지막의 숫자를 교체 한다. 9 <-> 40 1 2 3 4 5 6 7 8 4 8 6 7 3 1 5 2 9
c. 배열의 시작부터 교체 한 숫자 전 까지만 힙생성 알고리즘을 수행한다.0 1 2 3 4 5 6 7 8 8 7 6 4 3 1 5 2 9
d. a ~ c 과정을 반복 하여 마지막 수부터 정렬이 수행 된다. 아래는 정렬이 되는 과정이다.[8, 7, 6, 4, 3, 1, 5, 2, 9]
├───────┤ 힙정렬 구간
[7, 4, 6, 2, 3, 1, 5, 8, 9]
├──────┤ 힙정렬 구간
[6, 4, 5, 2, 3, 1, 7, 8, 9]
├─────┤ 힙정렬 구간
[5, 3, 4, 1, 2, 6, 7, 8, 9]
├────┤ 힙정렬 구간
[4, 2, 3, 1, 5, 6, 7, 8, 9]
├───┤ 힙정렬 구간
[3, 1, 2, 4, 5, 6, 7, 8, 9]
├──┤ 힙정렬 구간
[2, 1, 3, 4, 5, 6, 7, 8, 9]
├─┤ 힙정렬 구간
[1, 2, 3, 4, 5, 6, 7, 8, 9] <== 정렬 완료. -
시간 복잡도 : O(n log n)
-
힙정렬 알고리즘 애니메이션
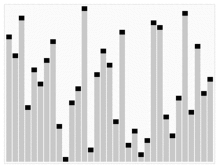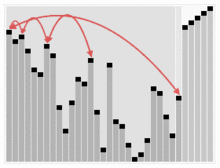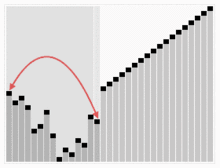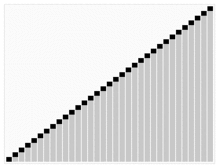
-
힙 정렬 알고리즘 자바 소스
public class HeapSort { public static void main(String[] args) { HeapSort(new int[] {3,5,1,2,4,8,6,9,7}); } private static void HeapSort(int[] nums) { //힙생성 알고리즘 수행 heapify(nums, 0, nums.length); //정렬 수행 for(int i = nums.length - 1; i >= 0; i--) { //가장큰 수인 첫번째 숫자와 가장 마지막 숫자의 자리를 교체 한다. swap(nums, 0, i); //배열의 첫번째 부터 교체된 인덱스까지 힙생성 알고리즘을 수행한다. heapify(nums, 0, i); } //출력 System.out.println(Arrays.toString(nums)); } //힙 생성 private static void heapify(int[] nums, int start, int end) { for (int i = start; i < end; i++) { int childIdx = i; while(childIdx != 0) { int rootIdx = (childIdx - 1) / 2; if(nums[rootIdx] < nums[childIdx]) { swap(nums, childIdx, rootIdx); } childIdx = rootIdx; } } } //인덱스 스왑 private static void swap(int[] nums, int child, int root) { int temp = nums[root]; nums[root] = nums[child]; nums[child] = temp; } }