정렬 알고리즘 기초4 - 병합 정렬(Merge Sort)

---

1. 병합 정렬 알고리즘(Merge Sort)

• 병합정렬은 분할 정복 알고리즘이다. 병합 정렬 알고리즘은 정확히 반씩 나누어 계산을 하기 때문에
  최악의 경우에도 O(n log n)의 동일한 속도를 보장 한다.

• 정렬 순서
  예1) 3,5,1,2,4,8,6,9,7,10 배열을 오름차순으로 정렬 하려고 할 경우

  1) 병합 정렬은 항상 반으로 쪼개어 정렬을 수행 한다. (2의 배수)

  0	1	2	3	4	5	6	7	8	9
  3	5	1	2	4	8	6	9	7	10

  1차
  

  0	1		2	3		4	5		6	7		8	9
  3	5		1	2		4	8		6	9		7	10

  2차
  

  0	1	2	3		4	5	6	7		8	9
  1	2	3	5		4	6	8	9		7	10

  3차
  

  0	1	2	3	4	5	6	7		8	9
  1	2	3	4	5	6	8	9		7	10

  4차
  

  0	1	2	3	4	5	6	7	8	9
  1	2	3	4	5	6	7	8	9	10

• 시간 복잡도 : O(n log n)

• 병합 정렬 알고리즘 애니메이션
  

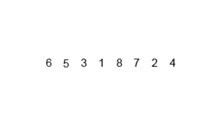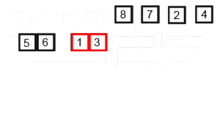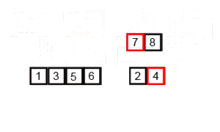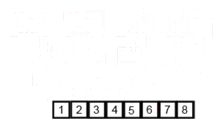
• 병합 정렬 알고리즘 자바 소스

  public class MergeSort {
    private static int[] sorted = new int[9];
  	
    public static void main(String[] args) {
        int[] numbers = { 3, 5, 1, 2, 4, 8, 6, 9, 7 };
        mergeSort(numbers, 0, numbers.length - 1);
        System.out.println(Arrays.toString(numbers));
    }
  	
    //정복
    public static void merge(int arr[], int left, int middle, int right) {
        int i = left;
        int j = middle + 1;
        int k = left;
  		
        while(i <= middle && j <= right) {
            if(arr[i] <= arr[j]) {
                sorted[k] = arr[i];
                i++;
            }else {
                sorted[k] = arr[j];
                j++;
            }
            k++;
        }
  		
        if(i > middle) {
            for(int t = j; t <= right; t++) {
                sorted[k] = arr[t];
                k++;
            }
        } else {
            for(int t = i; t <= middle; t++) {
                sorted[k] = arr[t];
                k++;
            }
        }
  		
        for(int t = left; t <= right; t++) {
            arr[t] = sorted[t];
        }
    }
  	
    //분할(재귀함수)
    public static void mergeSort(int arr[], int left, int right) {
        if(left < right) {
            int middle = (left + right) / 2;
            mergeSort(arr, left, middle);
            mergeSort(arr, middle + 1, right);
            merge(arr, left, middle, right);
        }
    }
  }