알고리즘 풀이 - 하노이 탑 이동(백준 알고리즘-재귀)

---

2020년 첫 알고리즘 풀이. 백준 알고리즘 문제의 재귀 카테고리에 있는 4가지 유형의 문제입니다.
재귀 알고리즘은 매우 기초적이지만 자주 헤깔릴 수 있는 알고리즘으로 아래 4가지 유형의 문제 풀이를 보고 되뇌여 보겠습니다.

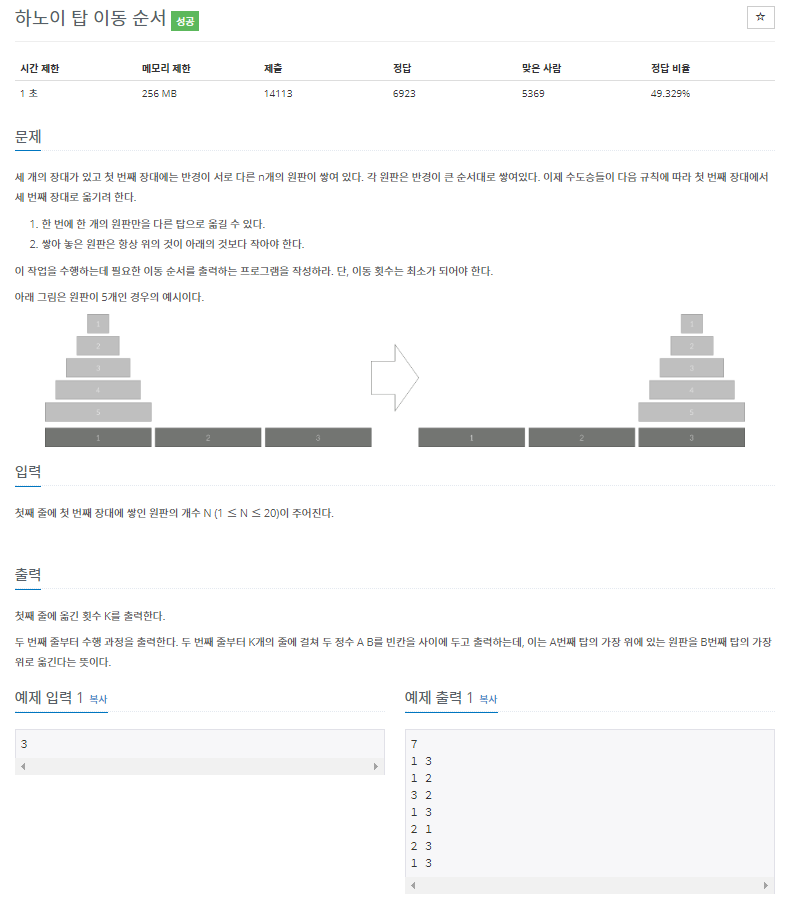
문제4 - 하노이 탑 이동 순서

문제 링크 : https://www.acmicpc.net/problem/11729

• 풀이

  • 하노이의 탑은 퍼즐을 일종으로 세 개의 기둥에 N개의 원판이 있고 주어진 기둥을고 모든 원판을 작은 원판이 위로 갈 수 있도록 이동 하는 게임입니다.

    • 우선 3개의 기둥을 설정 합니다.

      • 1번 기둥 : 이동 시작점
      • 2번 기둥 : 이동 임시 기둥
      • 3번 기둥 : 이동 완료 지점

    • hanoi 메소드는 4개의 파라메터를 받습니다(원판의 숫자, 시작위치, 임시위치, 완료위치)

    • 문제가 이동 하는 경로를 작성 하는 문제이므로 주어진 원판의숫자(N) 을 - 1 하면서 스택을 쌓습니다.

    • 쌓은 스택의 가장 마지막 원판의숫자(N) 이 1이 되는경우에는 완료위치(to) 로 이동 하였기 때문에 출력하고 해당 스택은 종료 합니다.

      • 처리되는 스택 정보의 일부를 작성 하면 아래와 같습니다.
        ※ IDE 디버깅 모드로 스택이 쌓여 가는 것을 참고하면 이해하기 편합니다.

            - 5, 1, 2, 3  
                └ 4, 1, 2, 3  
                    └ 3, 1, 2, 3  
                        └ 2, 1, 2, 3  
                            └ 1, 1, 2, 3 -> num == 1 return; print("1 3");  
                            └ print ("1 2");  
                            └ 1, 3, 1, 2 -> num == 1 return; print("3 2");  
                        └ print("1 3");  
                        └ 2, 2, 1, 3  
                            └ 1, 2, 3, 1 -> num == 1 return; print("2 1");  
                //......생략
      

• 소스

    public class Baekjoon_11729 {
        private static int cnt = 0;
        private static StringBuilder sb = new StringBuilder();
    	public static void main(String[] args) {
    		BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    		try {
    			int n = Integer.parseInt(reader.readLine());
    			hanoi(n, 1, 2, 3);
    			print();
    		} catch (Exception e) {
    			e.printStackTrace();
    		}
    	}
      
    	public static void hanoi(int num, int a, int b, int c) {
    		cnt++;
    		if(num == 1) {
    			sb.append(a +" "+ c + "\n");
    			return;
    		}else {
    			hanoi(num - 1, a, c, b);
    			sb.append(a +" "+ c + "\n");
    			hanoi(num - 1, b, a, c);
    		}
    	}
    
    	private static void print() {
            System.out.println(cnt);
            System.out.println(sb.toString());
        }
    }