알고리즘 풀이 - 동적계획법(백준-2748 피보나치 수 2)

이전 포스팅에서 알고리즘 문제중 재귀 문제 4가지를 확인 했습니다.
이번에는 동적 계획법을 통해서 어떻게 더 효율적으로 결과를 출력 할 수 있는지에 대해서 확인 해보겠습니다.

동적 계획법이란?

DP(Dynamic Programming) 특정 범위까지의 값을 구하기 위해서 그것과 다른 범위까지의 값을 이용하여 효율적으로 값을 구하는 알고리즘 설계 기법입니다.
이 알고리즘은 이미 계산된 값을 메모리에 저장 하고 메모리의 값을 재활용 하여 재귀 처리에 효율을 더한 알고리즘 입니다.
이 알고리즘을 이해 하는대에는 피보나치의 수 구하는 재귀 알고리즘의 스택을 보면 이해가 쉽습니다.

• 피보나치 수 (재귀)

    ─ fibonacci(5) 입력 -> fibonacci(4) + fibonacci(3) 처리
        └ fibonacci(4) -> fibonacci(3) + fibonacci(2) 처리
            └ fibonacci(3) -> fibonacci(2) + fibonacci(1) 처리      
                └ fibonacci(2) -> fibonacci(1) + fibonacci(0) 처리  
        └ fibonacci(3) -> fibonacci(2) + fibonacci(1) 처리          -- 중복계산
            └ fibonacci(2) -> fibonacci(1) + fibonacci(0) 처리      -- 중복계산
        ..........
  

  위에서 보이듯 fibonacci(5) 를 구하기 위해 처리 되는 재귀 호출의 스택에는 이미 계산된 중복 계산이 존재 하게 됩니다.
  이 중복된 계산을 미리 메모리에 저장 시켜 놓고 재활용 하는 방법을 동적 계획 법이라고 합니다.

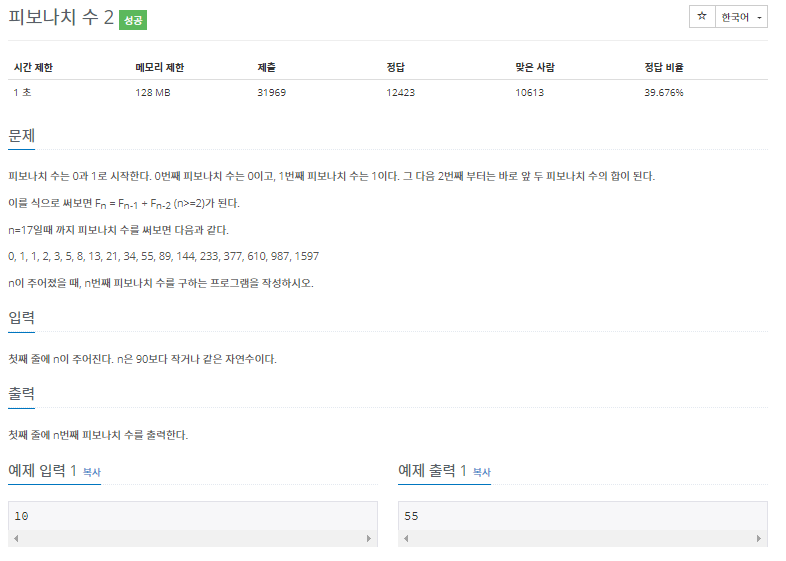
문제 - 피보나치의 수2 (백준 알고리즘)

문제 링크 : https://www.acmicpc.net/problem/2748

• 풀이

  • 기본 틀은 피보나치의 수 구하는 재귀 함수와 동일 합니다.
  • 계산된 값을 저장 하는 memo[] 배열이 추가 되어 값이 계산 될때 마다 해당 배열의 자리에 계산된 값을 입력 합니다.
  • 재귀 호출 되어 memo[n] 자리에 값이 있을 경우에는 재귀를 멈추고 해당 값을 return 합니다. (계산 생략으로 효율 상승)

• 풀이 소스

public class Baekjoon_2748 {
	public static void main(String[] args) {
		BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
		try {
			int n = Integer.parseInt(reader.readLine());
			memo = new long[n + 1];
			memo[1] = 1;
			System.out.println( fibonacci(n) );
		} catch (Exception e) {
			e.printStackTrace();
		}
	}
	
	private static long[] memo;
	public static long fibonacci(int n) {
		if(memo[n] > 0)
			return memo[n];
		if (n == 0)
			return 0;
		if (n == 1)
			return 1;
		memo[n] = fibonacci(n - 1) + fibonacci(n - 2);
		return memo[n];
	}
}