그래프 알고리즘 기초 - 플로이드 워셜 알고리즘(Floyd-Warshall)
By on November 22, 2023
그래프 알고리즘 기초 - 플로이드 워셜 알고리즘(Floyd-Warshall)
플로이드 워셜 알고리즘(Floyd-Warshall)
- 모든 노드의 최단 거리를 구할 수 있는 알고리즘.
- 참고사항
- 시간복잡도(노드수 : v) : O(V^3)
- 3중 for 문을 이용해서 모든 경로를 탐색 하기 때문에 속도가 느릴 수 밖에 없다.
- N = 1000개가 넘으면 10억번의 반복을 해야 하기 때문에 시간 초과 할 수 있다.
- 음수 가중치가 있는 경우에도 사용 가능.
- 핵심이해
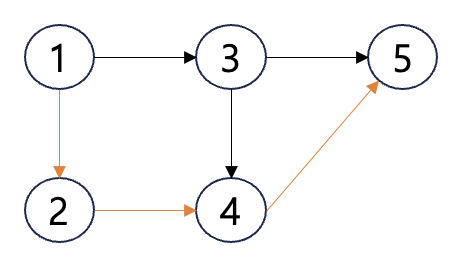
- 1 -> 2 -> 4 -> 5 로 가는 최단 경로의 그래프가 있는 경우가 있다고 생각 해보자.
- 1 -> 4로 가는 최단 경로는 1 -> 2 -> 4 일 수 밖에 없다.
- 공식 : D[S][E] = Math.min(D[S][E], D[S][K] + D[K][S])
- 알고리즘 활용 영역
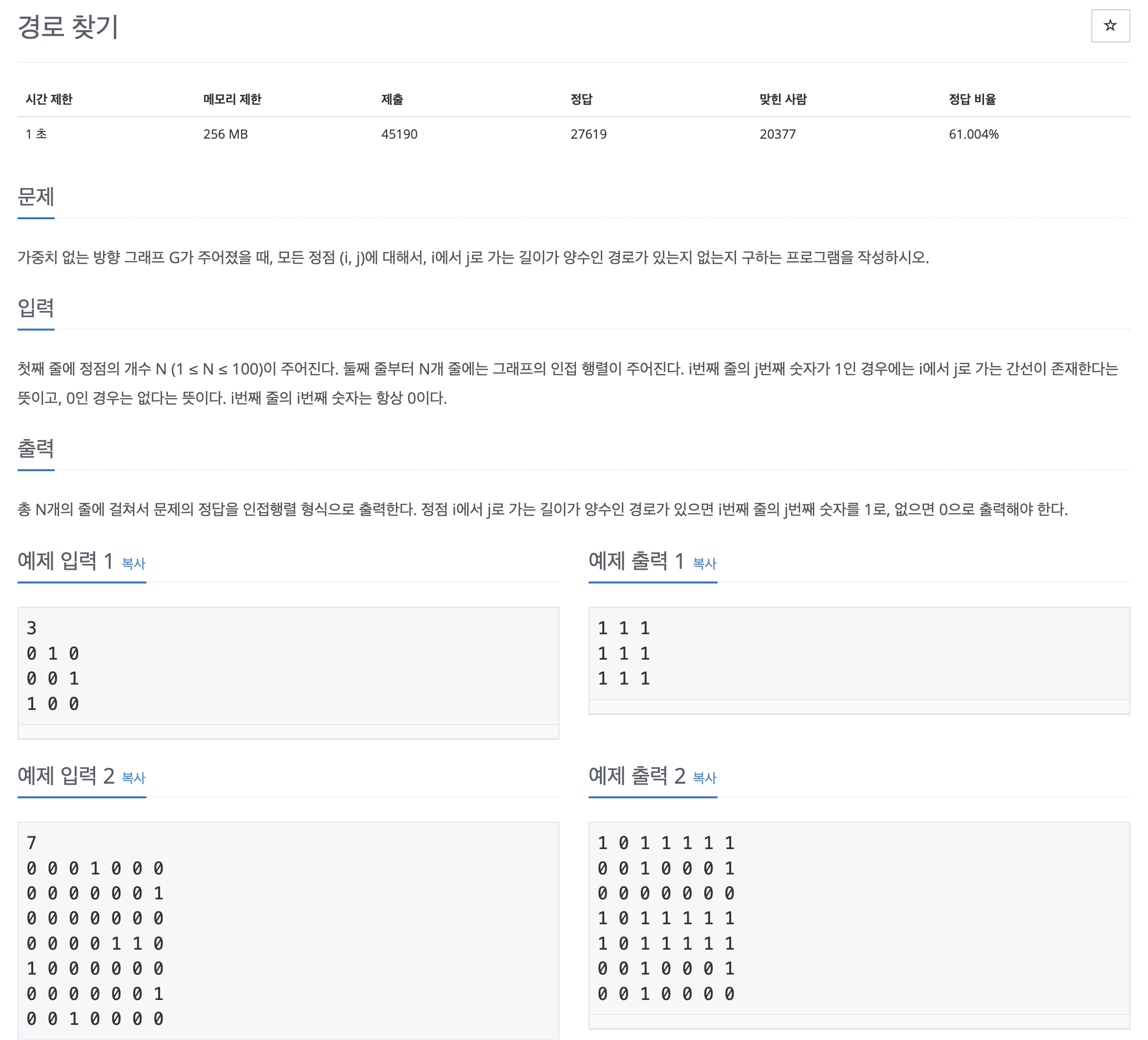
- 백준 11403 - 경로 찾기 https://www.acmicpc.net/problem/11403
플로이드 워셜 알고리즘(백준-경로 찾기)
public class BJ_11403 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[][] map = new int[n][n]; //2차원 배열 생성
for (int i = 0; i < n; i++) {
String[] input = br.readLine().split(" ");
for (int j = 0; j < n; j++) {
map[i][j] = Integer.parseInt(input[j]); //간선 입력
}
}
//3중 반복문 수행
for (int k = 0; k < n; k++) {
for (int s = 0; s < n; s++) {
for (int e = 0; e < n; e++) {
if(map[s][k] == 1 && map[k][e] == 1){
map[s][e] = 1;
}
}
}
}
//출력
for(int[] m : map){
System.out.println(Arrays.toString(m));
// 결과
// 1 1 1
// 1 1 1
// 1 1 1
}
}
}
풀이
입력 값을 그래프로 표현 하고 보면 플로이드워셜을 이해 하기가 쉽다.
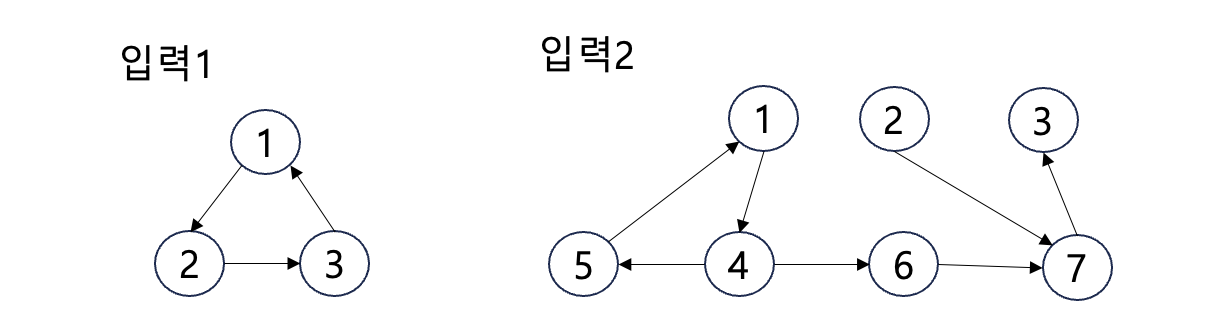
- 입력 1의 경우 이동 경로
- 1->2->3
- 2->3->1
- 3->1->2
위 경로로 이동이 가능하기 때문에 문제에서 요구 했던 i -> j 로 가는 경로를 1로 변경 하면 최종 결과를 확인 할 수 있다.